Describe Source of Errors in Solving Problems Using Numerical Method
There are two ways to minimize truncation error. Sation step and this can be solved by some.

Steady State Error What Is It And How To Calculate It Electrical4u
This chapter will describe some basic methods and techniques for programming simulations of differential equations.

. Describe the connection issue. Numerical methods and analysis. What are the reasons for developing errors in using numerical methods.
Answer 1 of 2. Bernier in Advances in Ground-Source Heat Pump Systems 2016 222 Numerical methods. Learn the principles of various numerical techniques for solving nonlinear equations performing integrations and solving differential equations by the Runge-Kutta methods.
This course focuses on conceptually understanding and implementing numerical techniques to solve mathematical problems. 1 use a higher order method and 2 use a ner grid so that points are closer together. Subjects Numerical analysis Problems exercises etc.
Second errors may arise from mistakes in programs themselves or in the measurement of physical quantities. Understanding of numerical methods is essential for all engineering students in order to develop a skill set for solving complex real world problems. First we will review some basic concepts of numerical approximations and then introduce Eulers method the simplest method.
The english language we use in. It starts with initial guess where the NRM is usually very good if and horrible if the guess are not close. Learn the alternative ways of using numerical methods to solve nonlinear equations perform integrations and solve differential equations.
Numerical di erentiation also has a truncation error as will the di erential equations methods we will study in Part IV which are based on numerical di erentiation formulas. And then present two different methods to solve it. Of the velocity of the car.
21B Numerical Solutions 6 EX 2 Use Newtons method to approximate a root of 7x32x-50 to 5 decimal places. In solving the problem by using the numerical method we already understand that the selection of the grid size strongly influences the calculation result so we must perform a grid independence. A system of linear or non-linear algebraic equations is produced from the discreti-.
It naturally finds applications in. It doesnt have to be something new simply presenting someone elses solution is acceptable. Find the value of if using.
Find the exact solution to the Initial Value Problem and use it to determine the exact. 83 Stability regions for multistep methods 141 84 Additional sources of difficulty 143 841 A-stability and L-stability 143 842 Time-varying problems and stability 145 85 Solving the finite-difference method 145 86 Computer codes 146 Problems 147 9 Implicit RK methods for stiff differential equations 149. Understanding of Question- From the question that you asked it is obvious that you are not the student of grade 10.
If you are planning to have a career in the field of engineering you need to understand the term numerical methods and acquire the best notes on Numerical Methods. The first part of the text introduces the necessary mathematical background the digital representation of numbers and different types of errors associated with numerical methods. It is only in relatively simple problems that such a.
This itself can create huge errors in determining the performance of the car no matter how accurate the numerical methods you may use are. Well Im taking Numerical Methods this semester also called Numerical Analysis in some places. Errors in deriving the mathematical equation or using a model that does not describe adequately the physical system under study Modelling error Selecting a wrong numerical method for solving a mathematical model.
Many problems in the real world are hard or impossible to solve analytically but easy to solve numerically. Selecting a wrong algorithm for implementing a numerical method. The general algorithm to solve such problem is shown in the diagram below.
We will provide details on algorithm development using the Euler method as an example. Analytical solutions are often too complicated and no-one has a useful solution. The present work deals with the use of asymptotic numerical methods ANM to manage crack onset and crack growth in the framework of Continuum Damage Mechanics CDM.
CiteSeerX - Document Details Isaac Councill Lee Giles Pradeep Teregowda. Nielsen Book Data Subjects. But in applications of numerical methods itself the two errors we.
Governing differential equations All fluid flow and heat exchange process are governed by three basic physical rules the mass conservation momentum conservation and energy conservation. Is the study of algorithms that use numerical approximation for the mathematical analysis. Numerical methods eg finite difference method finite element method finite volume method are not usually feasible for design purposesThis is due to the widely varying length-scales and time-scales that are necessary to treat the heat transfer in the borehole and.
Use technology see Technology Options below to approximate the solution to the Initial Value Problem using Eulers Method the Improved Eulers Method and the Runge-Kutta Method each with a step size See Project Requirements below for more details. You may have read so many books in english but dont think that you know all. The term-assignment is to find a real-life problem which is solvable by numerical methods.
Why are numerical methods important in scientific computation. NRM is usually home in on a root with devastating efficiency. Answer 1 of 2.
Up to 50 cash back Solving Problems with Numerical Methods. General process to solve a physic problem by numerical method 21. The second part explains how to solve typical problems using numerical methods.
Following points are the sources of error 1. Two thousand solved problems in numerical analysis. Newton-Raphson Method The Newton-Raphson method NRM is powerful numerical method based on the simple idea of linear approximation.
More specifically an application of regularization techniques to a 1D cohesive model is proposed. Numerical Methods Lecture Notes.

Error Intervals Gcse Maths Steps Examples Worksheet

Draft Surveys Methodology Calculations And Common Errors Thenavalarch

Margin Of Error Formula Examples 2 Youtube

Discretization Error An Overview Sciencedirect Topics

What Is Numerical Stability Nick Higham
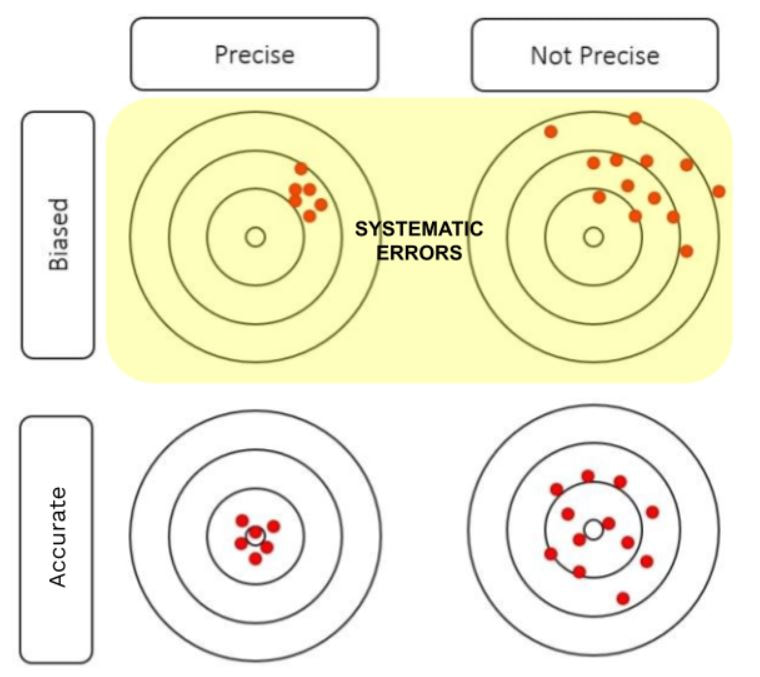
Error Analysis Biology For Life
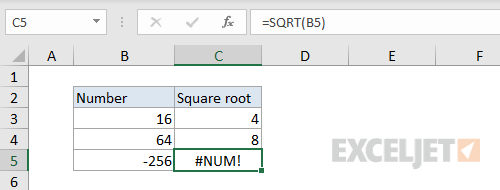
Excel Formula How To Fix The Num Error Exceljet

Gis Data A Look At Accuracy Precision And Types Of Errors Gis Lounge

Errors In Measurement Classification Of Errors Electrical4u

Floating Point Representation And Rounding Error Youtube

Numerical Methods Errors Introduction Wikibooks Open Books For An Open World
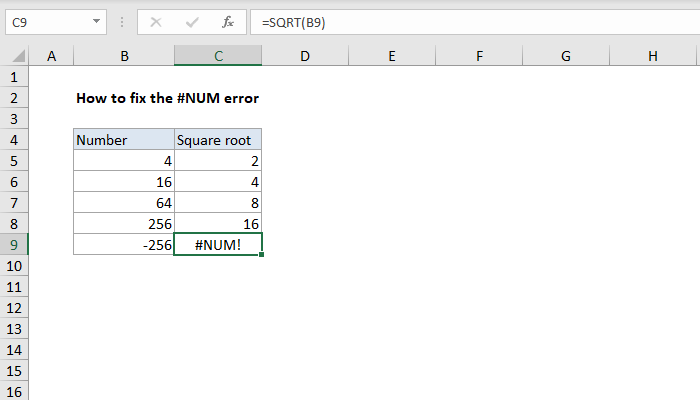
Excel Formula How To Fix The Num Error Exceljet

Trapezoid Rule Error Numerical Integration Approximation Youtube

Relative Error At Different Values T And X Download Table

How To Identify Type I And Type Ii Errors In Statistics Youtube

Hamming Code Error Detection Youtube

Powers Exponents Word Problems Error Analysis Find The Error Error Analysis Error Analysis Math Word Problems


Comments
Post a Comment